Tiger Algebra Calculator
Solving quadratic equations using the quadratic formula
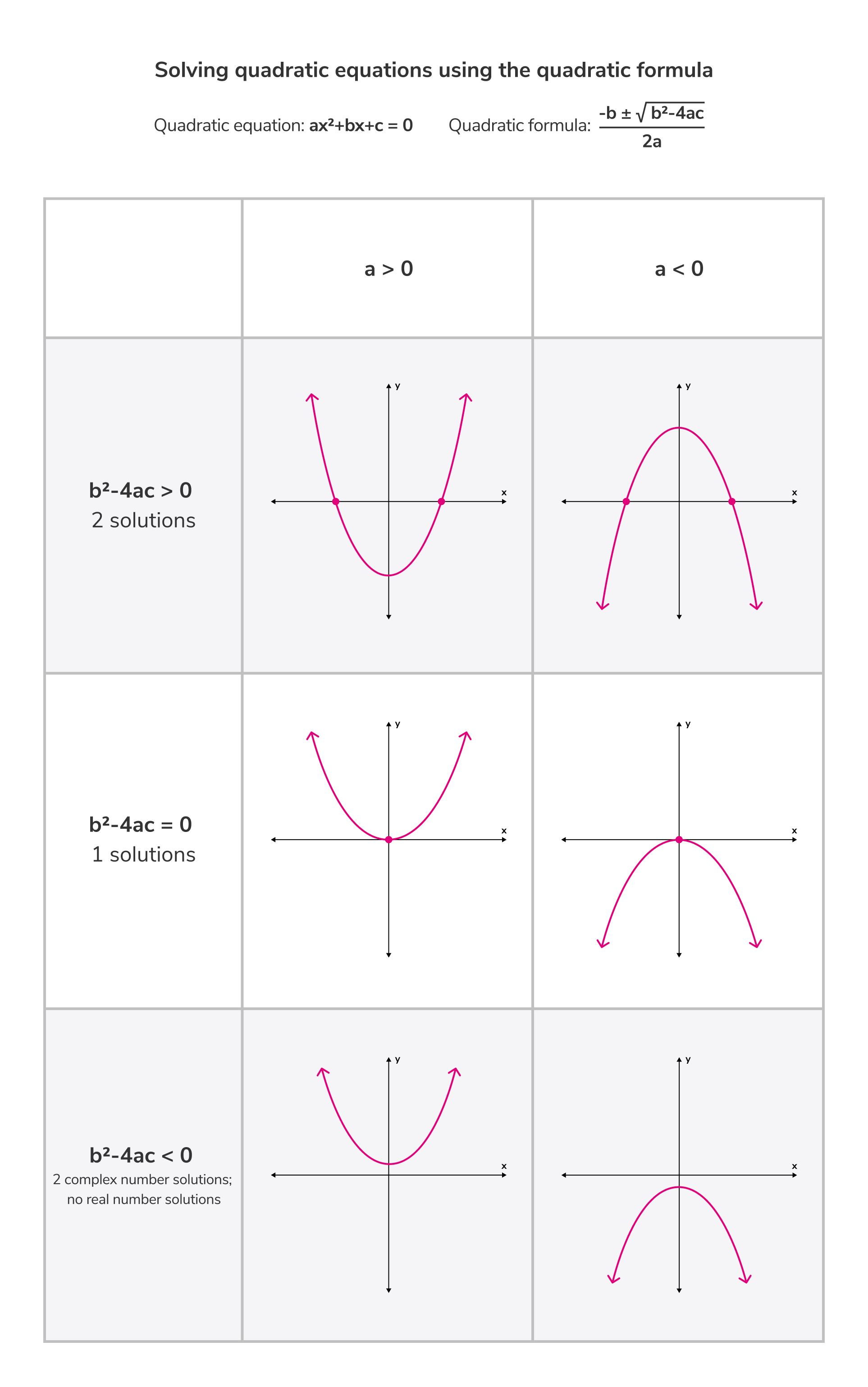
The solution(s), sometimes called roots or zeros, to a quadratic equation in its standard form, , can be found by plugging the equation's coefficients, a, b, and c, into the quadratic formula:
When plugged back into the original equation, these roots cause the equation to equal zero.
As the ± sign in the quadratic formula suggests, there can be two possible solutions, depending on the outcome of the formula's discriminant, , the part of the quadratic formula under the radical symbol. The binomial, , is called the discriminant because it discriminates between the possible solutions.
When plugged back into the original equation, these roots cause the equation to equal zero.
As the ± sign in the quadratic formula suggests, there can be two possible solutions, depending on the outcome of the formula's discriminant, , the part of the quadratic formula under the radical symbol. The binomial, , is called the discriminant because it discriminates between the possible solutions.
- If then the equation has two solutions.
- If then the equation has one solution.
- If then the equation has two complex numbers solutions. If you have not studied this topic yet, then you can probably assume there are no solutions for this equation.