Tiger Algebra Calculator
Finding a perpendicular line
Lines that are perpendicular intersect each other at a 90º angle. A plus symbol +, for example, is made up of two lines that run perpendicular to one another. The slopes of perpendicular lines are negative reciprocals of one another. For example: if a line has a slope of , then a line perpendicular to it would have a slope of .
Let's find the equation of a line perpendicular to that runs through the point . To do this, we can use either the point-slope or slope-intercept formula.
Slope-intercept form:
The slope-intercept form for the equation of a line is , in which represents the y-coordinate of a point on the line, represents the x-coordinate of the same point on the line, represents the slope of the line, and represents the y-intercept of the line, the point at which the line intersects the graph's y-axis.
Take the negative reciprocal of the line's slope, , to get , and plug it in for ; plug the x-coordinate, , in for ; plug the y-coordinate, , in for . This gives us , which simplifies to . We can then plug the slope () and y-intercept into the slope-intercept formula, , to get the equation of the line, .
Point-slope form:
The point-slope form for the equation of a line is , in which and represent the x and y-coordinates of a point on the line, and represent the x and y-coordinate of another point on the line, and represents the slope of the line. Take the negative reciprocal of the line's slope, , to get , and plug it in for ; plug the x-coordinate, , in for ; plug the y-coordinate, , in for . This gives us the equation of the line in point-slope form, .
Simplifying this further will give us the equation of the line in slope-intercept form.
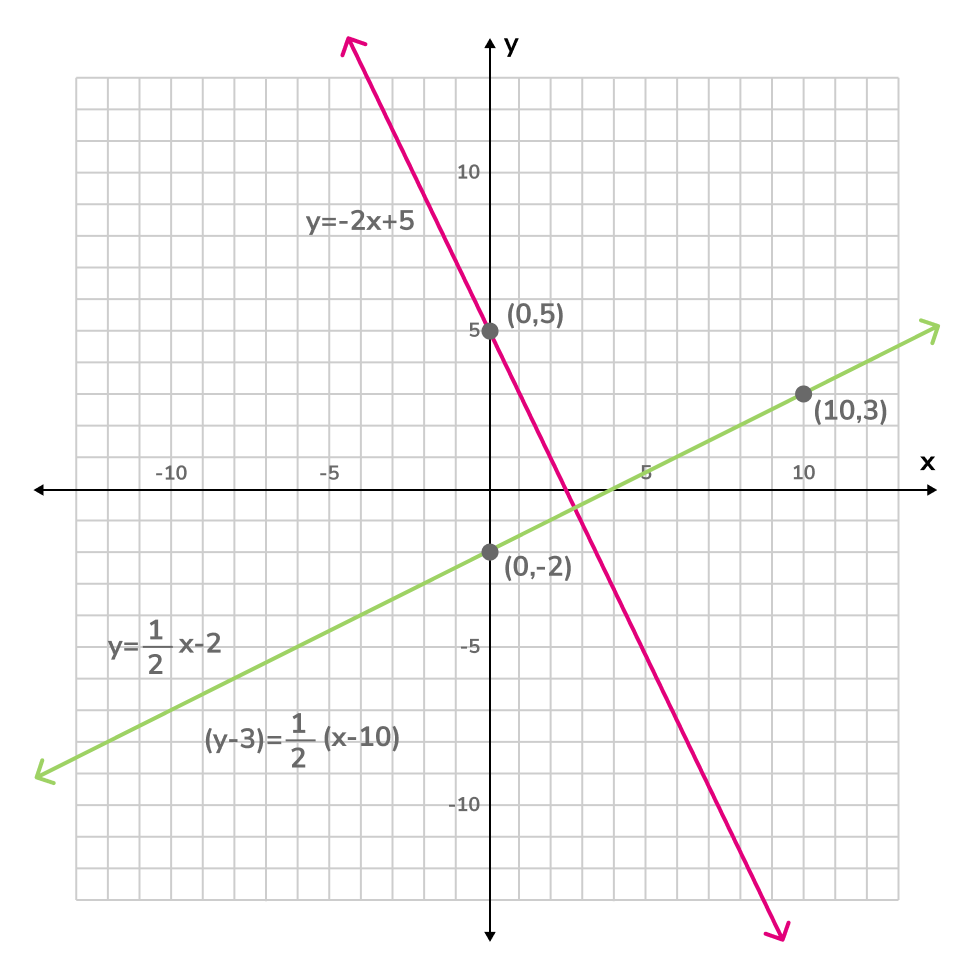
Let's find the equation of a line perpendicular to that runs through the point . To do this, we can use either the point-slope or slope-intercept formula.
Slope-intercept form:
The slope-intercept form for the equation of a line is , in which represents the y-coordinate of a point on the line, represents the x-coordinate of the same point on the line, represents the slope of the line, and represents the y-intercept of the line, the point at which the line intersects the graph's y-axis.
Take the negative reciprocal of the line's slope, , to get , and plug it in for ; plug the x-coordinate, , in for ; plug the y-coordinate, , in for . This gives us , which simplifies to . We can then plug the slope () and y-intercept into the slope-intercept formula, , to get the equation of the line, .
Point-slope form:
The point-slope form for the equation of a line is , in which and represent the x and y-coordinates of a point on the line, and represent the x and y-coordinate of another point on the line, and represents the slope of the line. Take the negative reciprocal of the line's slope, , to get , and plug it in for ; plug the x-coordinate, , in for ; plug the y-coordinate, , in for . This gives us the equation of the line in point-slope form, .
Simplifying this further will give us the equation of the line in slope-intercept form.

