Tiger Algebra Calculator
Systems of linear equations
Linear equations
A linear equation is an equation that represents a straight line. It usually has constants and variables, which cannot contain exponents or roots, and is usually written in one of the following ways:
Point-slope form
For example:
Slope-intercept form
For example:
Standard form
For example:
Important: In this form, and cannot both be zero ().
Though these equations may all look different, they all actually represent the same line. If you have access to a graphing calculator, try graphing each equation and comparing the results. The graphs will all be the same!
Systems of linear equations
Sometimes we are given two or more equations that can be made true by the same variable or variables.
For example:
When and , both equations are true.
These are called systems of linear equations and we can find their variable(s) using one of two methods: elimination and substitution.
Solving by elimination
Main steps for solving a system of linear equations by elimination:
1. Rewrite the equations so the variables are in the same order:
would become
2. Multiply one or both of the equations by non-zero numbers that would make one set of terms cancel each other out if added or subtracted:
would become
3. Add or subtract the equations to eliminate their common variable:
4. Solve the equation to isolate the remaining variable:
5. Plug this variable into one of the original equations and simplify to isolate the remaining variable:
The variables that satisfy both equations are and or
6. Repeat as necessary, such as when there are more than two linear equations in the system.
Solving by substitution
Main steps for solving a system of linear equations by substitution:
1. Solve for or in one of the equations by isolating the variable:
2. Plug the resulting variable into the other equation and solve:
3. Plug the resulting variable into either of the original equations and solve:
The variables that satisfy both equations are and or
4. Repeat as necessary, such as when there are more than two linear equations in the system.
There are three possible solution types for systems of linear equations:
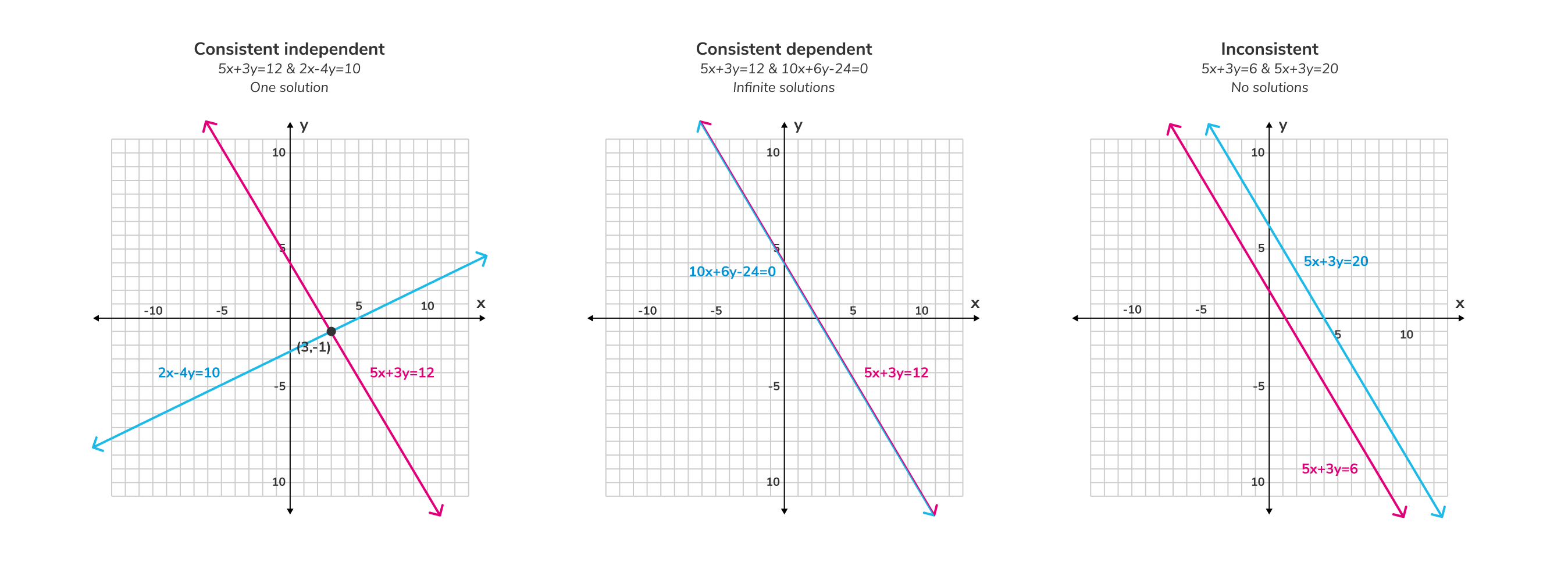
No solution : There are no variables that would make all the equations in the system true. On a graph, the lines representing the equations do not touch. If they are linear equations, these lines would run parallel to each other.
One solution : There is one set of variables that would make all the equations in the system true. On a graph, the lines representing the equations cross once. The point where they cross is the solution to the system.
Infinite solutions : There are an infinite number of variables that would make all the equations in the systems true. This occurs when all the equations in the system are the same or are variations of the same equation and, therefore, represent the same line.
Other relevant terms:
Consistent equations : two or more equations are consistent when they share one or infinite solutions. For example: and are consistent because they share one solution .
Inconsistent equations : two or more equations are inconsistent when they do not share any solutions, meaning their lines have no points in common. The lines of inconsistent equations run parallel to each other. For example: and are inconsistent because has a different value in each equation, meaning the equations do not share any solutions.
Independent equations : two or more equations are independent when they represent different lines.
Dependent equations : two or more equations are dependent when they represent the same line, giving each equation infinite solutions. Dependent equations occur when an equation is written in different forms. For example: and represent the same line and are, therefore, dependent.
A linear equation is an equation that represents a straight line. It usually has constants and variables, which cannot contain exponents or roots, and is usually written in one of the following ways:
Point-slope form
For example:
Slope-intercept form
For example:
Standard form
For example:
Important: In this form, and cannot both be zero ().
Though these equations may all look different, they all actually represent the same line. If you have access to a graphing calculator, try graphing each equation and comparing the results. The graphs will all be the same!
Systems of linear equations
Sometimes we are given two or more equations that can be made true by the same variable or variables.
For example:
When and , both equations are true.
These are called systems of linear equations and we can find their variable(s) using one of two methods: elimination and substitution.
Solving by elimination
Main steps for solving a system of linear equations by elimination:
1. Rewrite the equations so the variables are in the same order:
would become
2. Multiply one or both of the equations by non-zero numbers that would make one set of terms cancel each other out if added or subtracted:
would become
3. Add or subtract the equations to eliminate their common variable:
4. Solve the equation to isolate the remaining variable:
5. Plug this variable into one of the original equations and simplify to isolate the remaining variable:
The variables that satisfy both equations are and or
6. Repeat as necessary, such as when there are more than two linear equations in the system.
Solving by substitution
Main steps for solving a system of linear equations by substitution:
1. Solve for or in one of the equations by isolating the variable:
2. Plug the resulting variable into the other equation and solve:
3. Plug the resulting variable into either of the original equations and solve:
The variables that satisfy both equations are and or
4. Repeat as necessary, such as when there are more than two linear equations in the system.
There are three possible solution types for systems of linear equations:
No solution : There are no variables that would make all the equations in the system true. On a graph, the lines representing the equations do not touch. If they are linear equations, these lines would run parallel to each other.
One solution : There is one set of variables that would make all the equations in the system true. On a graph, the lines representing the equations cross once. The point where they cross is the solution to the system.
Infinite solutions : There are an infinite number of variables that would make all the equations in the systems true. This occurs when all the equations in the system are the same or are variations of the same equation and, therefore, represent the same line.
Other relevant terms:
Consistent equations : two or more equations are consistent when they share one or infinite solutions. For example: and are consistent because they share one solution .
Inconsistent equations : two or more equations are inconsistent when they do not share any solutions, meaning their lines have no points in common. The lines of inconsistent equations run parallel to each other. For example: and are inconsistent because has a different value in each equation, meaning the equations do not share any solutions.
Independent equations : two or more equations are independent when they represent different lines.
Dependent equations : two or more equations are dependent when they represent the same line, giving each equation infinite solutions. Dependent equations occur when an equation is written in different forms. For example: and represent the same line and are, therefore, dependent.

