Tiger Algebra Calculator

Properties of ellipses

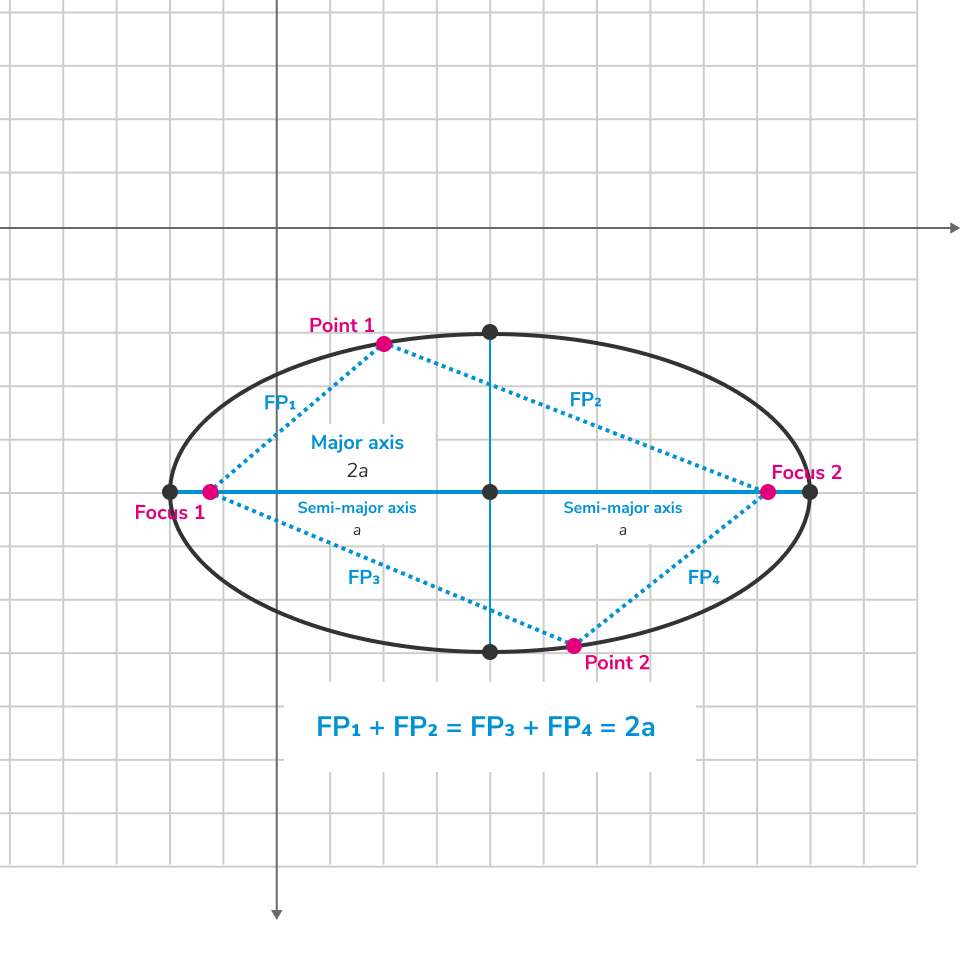
An ellipse is the set of all points on a plane whose distances from two fixed points, called focus points or foci, add up to a constant value that is equal to the length of the major axis of the ellipse.

For example, let's say we have a major axis that is

12

units long. The foci of the ellipse always lie on the major axis. The ellipse itself would be formed by imaginary lines from both foci to the same point on the ellipse, such that their total lengths equal

12

, the length of the major axis. The lengths of the lines could be

6

and

6

4

and

8

1.5

and

10.5

, or literally any combination of positive rational numbers that add up to

12

, of which there are an infinite number.
definition

Standard form

Standard form of a horizontal ellipse: $\frac{{(x - h)}^{2}}{a^{2}} + \frac{{(y - k)}^{2}}{b^{2}} = 1$
Standard form of a vertical ellipse: $\frac{{(x - h)}^{2}}{b^{2}} + \frac{{(y - k)}^{2}}{a^{2}} = 1$

Note: The standard form equation of an ellipse is made of two fractions, in which

a^{2}

is the larger of the two denominators and

b^{2}

is the smaller of the two denominators. The standard form of an ellipse requires that the right side of the equation equal

1

Points

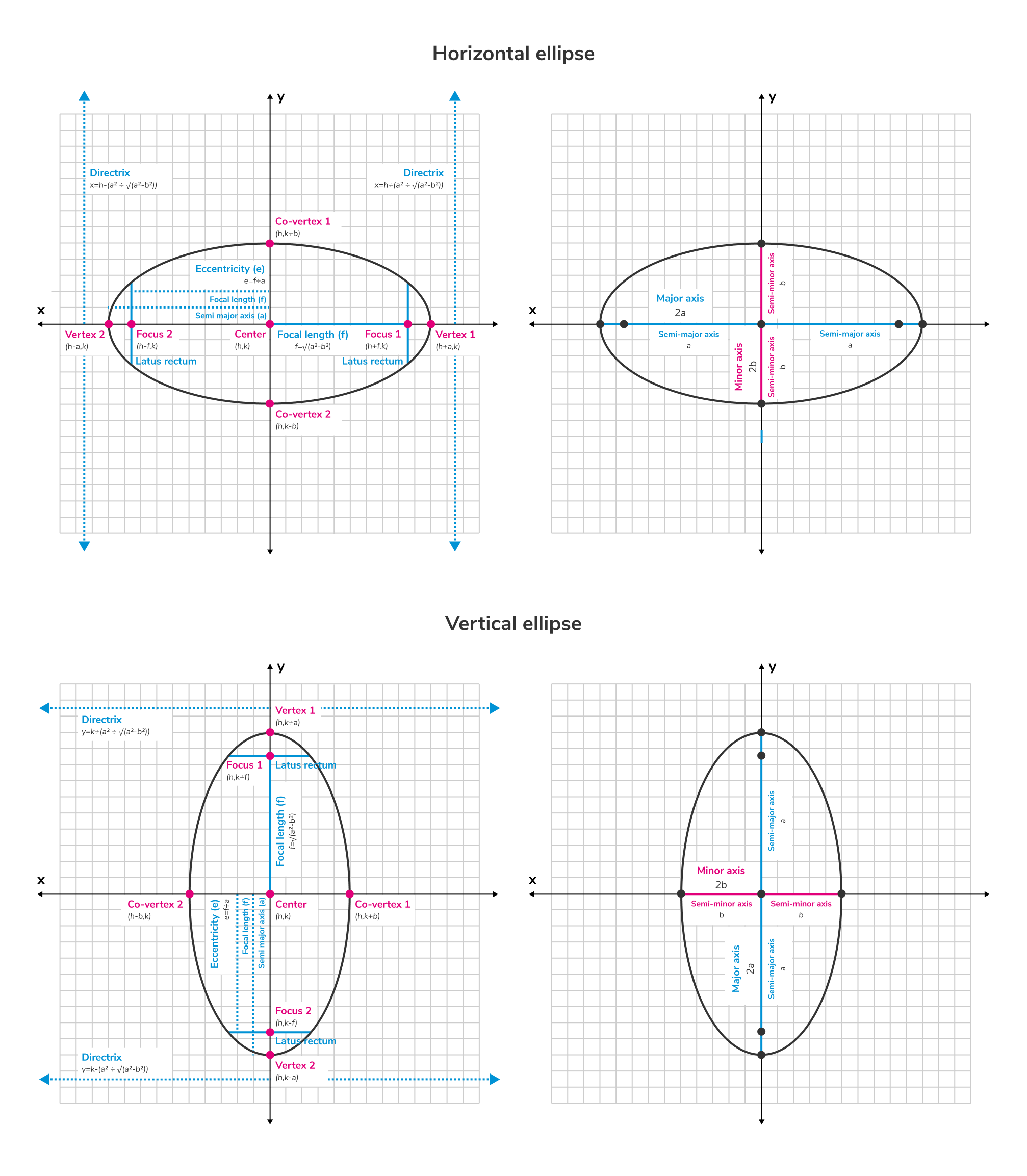
Center $(h, k)$ : The point in the center of an ellipse. $h$ represents the x-coordinate and $k$ represents the y-coordinate.
Vertices: The intersections of the major axis with the ellipse.
Co-vertices: The intersections of the minor axis with the ellipse.

Lines, line segments, and axes

The major axis $(2 a)$ : the longer of the two axes that make up an ellipse. It runs from one side of the ellipse, through its center, to the other side of the ellipse at its widest point.
The minor axis $(2 b)$ : the shorter of the two axes that make up an ellipse. It runs perpendicular to the major axis, from one side of the ellipse, through its center, to the other side of the ellipse.
Semi-major axis $(a)$ : half the length of the major axis.
Semi-minor axis $(b)$ : half the length of the minor axis.
Focal length $(f)$ : the distance from the center of an ellipse to one of its foci. $f = \sqrt{a^{2} - b^{2}}$
Focal parameter $(p)$ : the distance from a focus to the corresponding directrix. $p = \frac{b^{2}}{\sqrt{a^{2} - b^{2}}}$
Directrix: Two lines outside of the ellipse that run perpendicular to the major axis and are used in conjunction with the foci to define the ellipse.
In a horizontal ellipse: $x = h \pm \frac{a^{2}}{\sqrt{a^{2} - b^{2}}}$
In a vertical ellipse: $y = k \pm \frac{a^{2}}{\sqrt{a^{2} - b^{2}}}$ .
Latus rectum: The line segments that run perpendicular to the major axis, through the foci, such that their endpoints lie on the ellipse. Their lengths equal $\frac{2 \cdot b^{2}}{a}$ .

Other properties

Area: $π \cdot a \cdot b$
Eccentricity $(e)$ : A measure of how elongated an ellipse is, defined by the following ratio: 1. The distance from the center to either focus to 2. The distance from the center to either vertex: $\frac{\sqrt{(a^{2} - b^{2})}}{a}$
The eccentricity of an ellipse is always between $0$ and $1 (0 < e < 1)$ .

Latest Related Drills Solved

1 »