Tiger Algebra Calculator

A straight line is a one-dimensional figure that has a minimal thickness and extends infinitely in two opposing directions.
Every straight line has a slope that represents its gradient, or steepness. In mathematical expressions, this is typically written as $$m$$ and we can calculate it by selecting two points on the line and dividing the difference in their y-coordinates by the difference in their x-coordinates. The change in a line's y-coordinates represents the line's vertical change and is often referred to as the "rise", whereas the change in a line's x-coordinates represents the line's horizontal change and is often referred to as the "run". This means the slope of a straight line is equal to the line's rise divided by its run $$m=\left(y_2-y_1\right)/\left(x_2-x_1\right)=△y/△x$$.

Here are some other useful facts about straight lines:

• A straight line is the shortest distance between any two points.
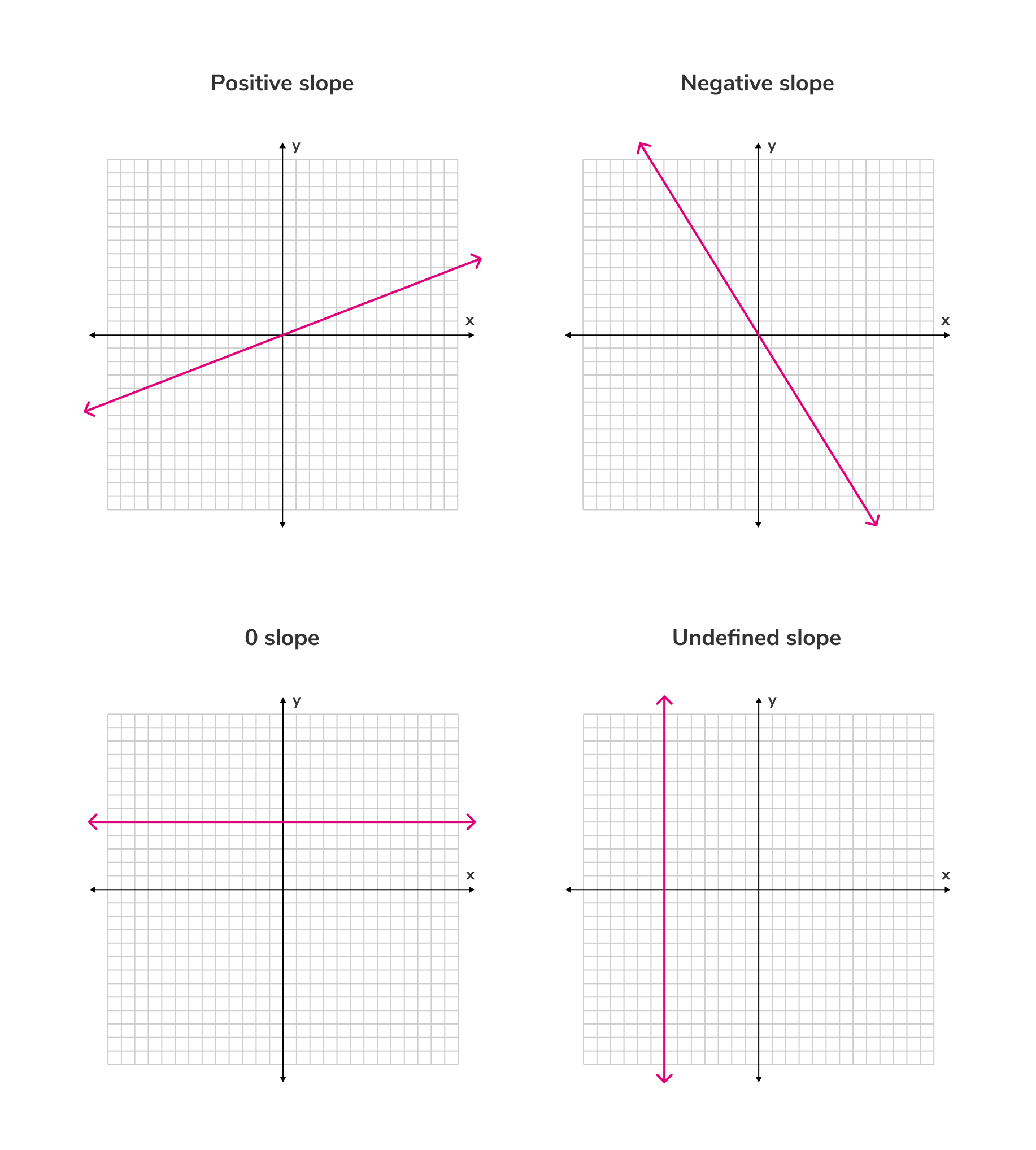
• If a line rises to the right, then its slope is positive.
• If a line falls to the right, then its slope is negative.
• A line that rises to the right at a 45° angle has a slope of 1.
• A line that falls to the right at a 45° angle has a slope of -1.
• A horizontal line has a slope of 0.
• A vertical line has an undefined slope.

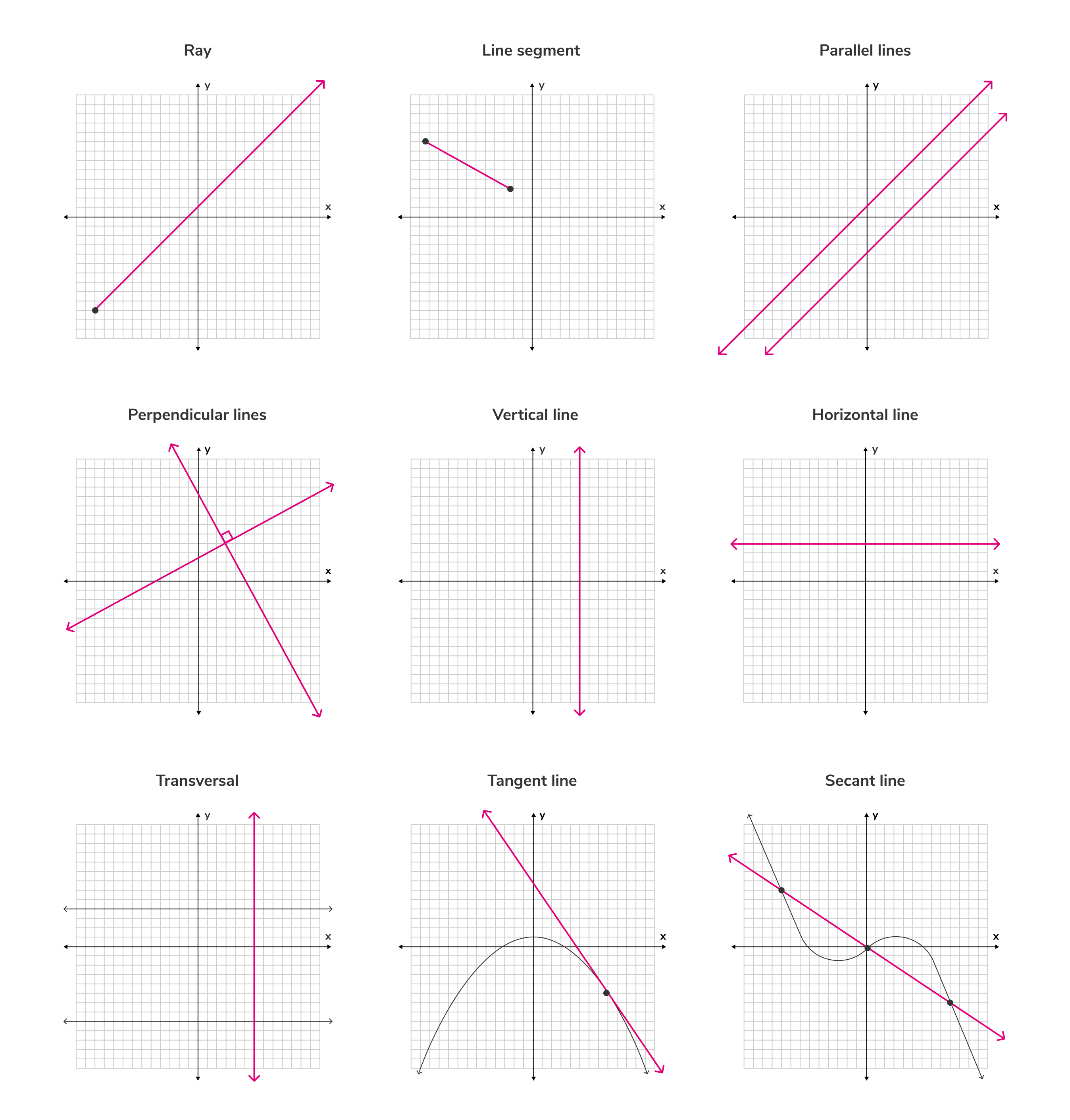
Types of lines:

• Ray: A line with one fixed end and one end that continues forever.
• Line segment: A line with two fixed ends.
• Parallel lines: Two or more lines that have the same slope and, therefore, never meet.
• Perpendicular lines: Two lines that intersect at a right angle (90°). Their slopes are negative reciprocals of one another.
• Vertical line: A line that runs parallel to a plane's y-axis. The slope of a vertical line is undefined.
• Horizontal line: A line that runs parallel to a plane's x-axis. The slope of a vertical line is 0.
• Transversal: A line that crosses at least two other lines.
• Tangent line: A line that touches a curve, matching the curve's slope at that point.
• Secant line: A line that intersects two or more points on a curve.

Equations of lines: A linear equation is the equation of a straight line. Linear equations most commonly take the following forms:

• Standard form: $$ax+by=c$$ in which $$x$$ and $$y$$ represent the x and y-coordinates of a point on the line and $$a,b$$ and $$c$$ represent coefficients. If $$a=0$$ then $$b\ne 0$$ and if $$b=0$$ then $$a\ne 0$$.
• Slope-intercept form: $$y=mx+b$$ in which $$x$$ and $$y$$ represent the coordinates of a point on the line, $$m$$ represents the slope, and $$b$$ represents the y-Intercept, the value of $$y$$ when $$x$$ equals $$0$$.
• Point-slope form: $$y-y_1=m\left(x-x_1\right)$$ in which $$x$$ and $$x_1$$ represent the x-coordinates of two points on a line, $$y$$ and $$y_1$$ represent the y-coordinates of two points on a line, and $$m$$ represents the slope of a line.
• Equation of a vertical line: The exception to this is when a line is vertical, in which case its slope is undefined and the line cannot be represented by slope-intercept or point-slope form. The equation of such lines is $$x=$$?. All the points on vertical lines have the same x-coordinate so we define the line in terms of its x-variable.

Relevant terms:

• y-intercept: The point on a graph where a line crosses the graph's y-axis. It is also the value of $$y$$ when $$x$$ equals $$0$$.
• x-Intercept: The point on a graph where a line crosses the graph's x-axis. It is also the value of $$x$$ when $$y$$ equals $$0$$.