Tiger Algebra Calculator

Parabola

A parabola is a curve made up of all the points on a graph that are the same distance from a given point, the focus, as they are from a given line, the directrix.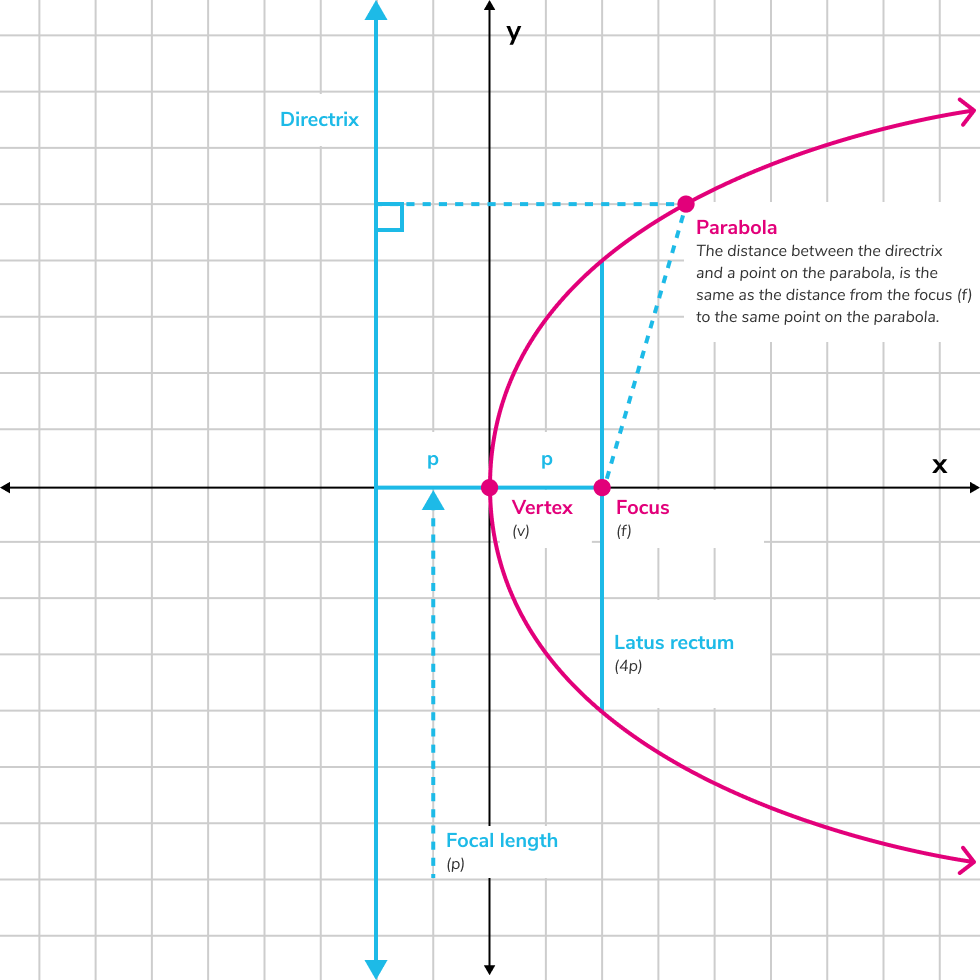

Important concepts:

Standard form

• Standard form of a horizontal parabola: $$x=a{y}^2+by+c$$; if $$a<0$$ then the parabola opens to the left; if $$a>0$$ then the parabola opens to the right.
• Standard form of a vertical parabola: $$y=a{x}^2+bx+c$$; if $$a<0$$ then the parabola opens downward like a frown; if $$a>0$$ then the parabola opens upward like a smile.

Vertex form
The vertex of a parabola is usually represented by $$h$$ (for the x-coordinate) and $$k$$ (for the y-coordinate), which can be found using the vertex form. In the vertex form for both horizontal and vertical parabolas, $$a$$ represents a reflection across the x-axis and/or a vertical stretch or compression, $$h$$ represents a horizontal translation (a shift to the left or right), and $$k$$ represents a vertical translation (a shift up or down).

• Vertex form of a horizontal parabola: $$x=a{\left(y-k\right)}^2+h$$, in which ; if $$a<0$$ then the vertex is on the right, and the parabola opens to the left; if $$a>0$$ then the vertex is on the left, and the parabola opens to the right.
• Vertex form of a vertical parabola: $$y=a{\left(x-h\right)}^2+k$$; if $$a<0$$ then the vertex is the highest point; if $$a>0$$ then then the vertex is the lowest point.

Points

• Vertex $$\left(h,k\right)$$: The origin point of a parabola that is located between the directrix and focus. The vertex form (see Vertex form) can be used to find the vertex of horizontal and vertical parabolas.
• Focus $$\left(h\pm p,k\right)\left(h,k\pm p\right)$$: A parabola's focus is a point that is located within the curve of the parabola that the parabola bends around. The distances from the focus and directrix to any point on the hyperbola are the same.

Lines, line segments, and axes

• Axis of symmetry: A line that runs through the vertex of a parabola, creating two congruent halves.
• Directrix: A line that runs perpendicular to a parabola's axis of symmetry and parallel to its latus rectum. The distance from a parabola's vertex to its directrix is the same as the distance from the parabola's vertex to its focus.
• Focal length $$\left(p\right)$$: The distance between the parabola's vertex and focus. This distance is equal to the distance between the parabola's vertex and directrix.
• Latus rectum $$\left(4p\right)$$: A line segment located inside the parabola that runs through the parabola's focus and that is perpendicular to the parabola's axis of symmetry. The length of the latus rectum is equal to four times the parabola's focal length and can be expressed as $$4p$$.