Tiger Algebra Calculator

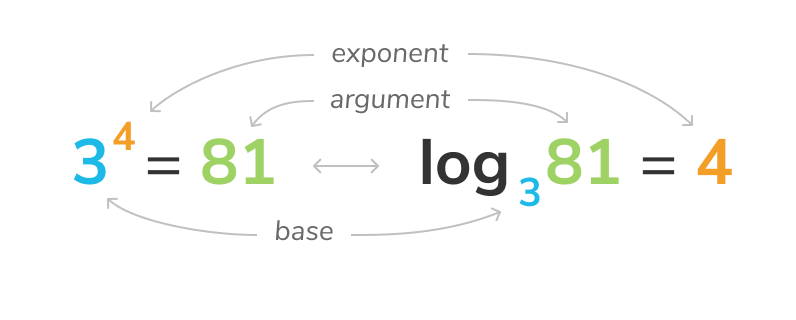
Logarithms answer the question: "what exponent do we need to raise a specified number by to turn it into another specified number ?" or, more simply, "how many times do we need to multiply a number by itself to get another specified number ?" For example: What exponent do we need to raise $$3$$ by for it to become $$81$$ or how many times do we need to multiply $$3$$ by itself to get $$81$$? The answer is $$4$$, making the equation for this problem $$lo{g}_{3}81=4$$. Spoken out loud, this would be: "the logarithm of $$81$$ with base $$3$$ equals $$4$$ or log base $$3$$ of $$81$$ is $$4$$ or the base $$3$$ log of $$81$$ is $$4$$.

The number that we multiply by itself is called the base of the logarithm. In our example, $$3$$ is the base of the logarithm.
The number between the base and the = sign is called the argument and is the number we get when we raise the base of the log ($$3$$) to the equation's solution ($$4$$). In our example, $$81$$ is the argument.
The solution of the log is the exponent to which we raise the base of the log to get the logarithm's argument. In our example, $$4$$ is the solution.

A logarithm written with no base usually has a base of $$10$$ and is called a common logarithm. For example, $$log100=lo{g}_{10}100$$
The log button on calculators inputs the common logarithm.
Natural logarithms, on the other hand, are written as ln and are logs with a base of $$e$$. In this context, $$e$$ represents Euler's Number, an irrational number that equals approximately 2.7182. We can input a natural logarithm on a calculator by pressing the ln button.

Logarithms can also be positive or negative and include decimals.

Properties of logarithms with the same base:

Product rule: $$lo{g}_{a}x+lo{g}_{a}y=lo{g}_a\left(x·y\right)$$
Quotient rule: $$lo{g}_{a}x-lo{g}_{a}y=lo{g}_a\left(\frac{x}{y}\right)$$
Power rule: $$lo{g}_a\left(x^b\right)=b·lo{g}_{a}x$$
Inverse rule: $$-lo{g}_{a}x=lo{g}_a\left(\frac{1}{x}\right)$$
Equality rule: If $$lo{g}_{a}x=lo{g}_{a}y$$ then $$x=y$$


Changing of base properties:

$$lo{g}_{a}x=\frac{lo{g}_{b}x}{lo{g}_{b}a}$$

$$lo{g}_{a}x=\frac{1}{lo{g}_{x}a}$$


The relationship between logarithms, exponents, and roots:
If we wrote an exponential equation three times, each time replacing a different value with a variable, we would get three very different, but closely related equations.
Let's look at the exponential equation: $$3^4=81$$.

Scenario 1: Replacing the solution with a variable
Replacing the solution with $$x$$ would give us $$3^4=x$$, which simplifies to $$x=81$$

Scenario 2: Replacing the exponent with a variable
Replacing the exponent with $$x$$ would give us $$3^x=81$$, which is a logarithmic equation that could be rewritten as $$lo{g}_{3}81=x$$ and simplified as $$x=4$$

Scenario 3: Replacing the base with a variable
Replacing the base with $$x$$ would give us $$x^4=81$$, which could be rewritten as $$\sqrt[4]{81}=x$$ and simplified as $$x=3$$