Tiger Algebra Calculator
Distance between two points
The distance formula, an application of the Pythagorean theorem, is a very helpful tool for finding the distance between two points. The Pythagorean theorem states the following: in a right triangle, the length of side squared plus the length of side squared is equal to the length of the hypotenuse (side ) squared.
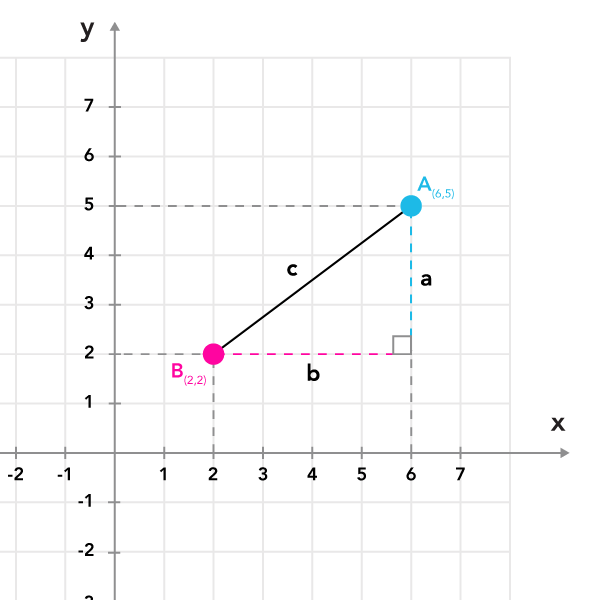
The hypotenuse () is the longest side of a right triangle and is always opposite the right angle. The length of the hypotenuse also represents the distance between points A and B, which can each be represented by two coordinates: an coordinate and a coordinate.
Point A =
Point B =
To get the distance formula, we can rewrite the Pythagorean theorem as:
in which represents the distance between points A and B, and the Xs and Ys represent the and coordinates of points A and B.
In order to find the distance between two points, enter their coordinates (for example (1,2) and (3,4)) and click the solve button.

The hypotenuse () is the longest side of a right triangle and is always opposite the right angle. The length of the hypotenuse also represents the distance between points A and B, which can each be represented by two coordinates: an coordinate and a coordinate.
Point A =
Point B =
To get the distance formula, we can rewrite the Pythagorean theorem as:
in which represents the distance between points A and B, and the Xs and Ys represent the and coordinates of points A and B.
In order to find the distance between two points, enter their coordinates (for example (1,2) and (3,4)) and click the solve button.
