Tiger Algebra Calculator
No solutions found
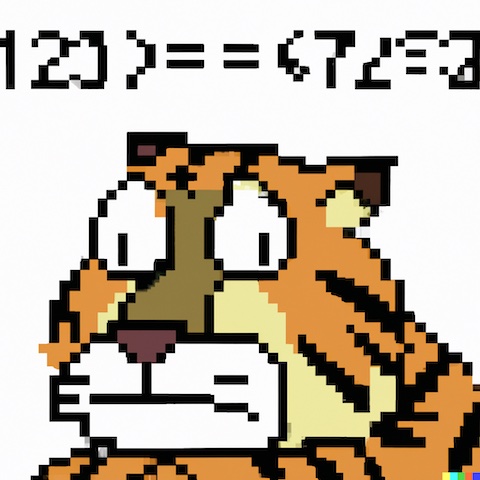
Try this:
- Check out our <a href="/en/terms-and-topics/formatting-guide/">formatting guide</a>
- Check out our formatting guide
- Check your input for typos
- Contact us
- Let us know how we can solve this better
We are constantly updating the types of the problems Tiger can solve, so the solutions you are looking for could be coming soon!
Other Ways to Solve
Tiger Algebra CalculatorHow did we do?
Please leave us feedback.